Kết quả thi học sinh giỏi lớp 9 Hà Nội 2016

Kỳ thi học sinh giỏi lớp 9 thành phố Hà Nội được tổ chức ngày 14 tháng 4 năm 2016. Các môn văn hóa được tổ chức dự thi bao gồm: Ngữ Văn, Lịch sử, Địa Lý, Toán học, Vật lý, Hóa học, Sinh học, Tin học, tiếng Anh, tiếng Pháp, Giáo dục Công dân.

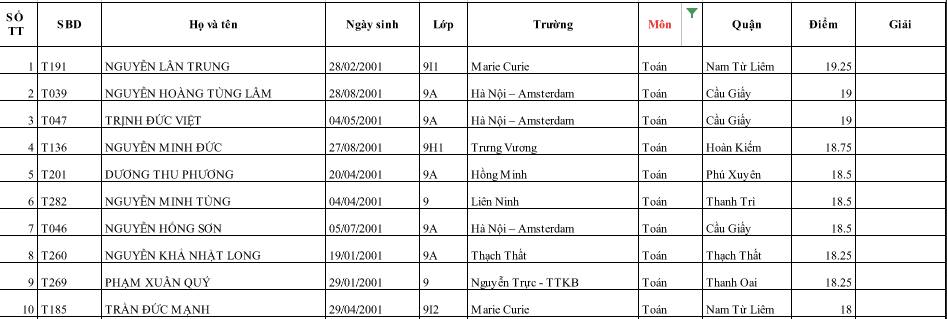
Danh sách 10 thí sinh có kết quả tốt nhất môn Toán

Danh sách đầy đủ xem tại ĐÂY (tệp EXCEL).

Kết quả chọn IJSO xem tại ĐÂY.

Đề thi học sinh giỏi môn toán thành phố Hà Nội 2016

1. Cho các số nguyên $a,b,c,d$ thõa mãn $a^3+b^3=2(c^3-8d^3)$. Chứng minh rằng $a+b+c+d$ chia hết cho 3.
2. Tìm tất cả các số nguyên tố $x$ sao cho $2^x+x^2$ là số nguyên tố.
3. Giải phương trình $\sqrt{2x^2+11x+19}+\sqrt{2x^2+5x+7}=3(x+2)$.
4. Tìm tất cả các bộ ba số $x,y,z$ thỏa mãn $x+y+z=3$, $1/x+1/y+1/z=1/3$  và $x^2+y^2+z^2=17$.
5. Cho ba số dương $x,y,z$ nhỏ hơn $\sqrt3/2$  và thỏa mãn $xy+yz+zx=3/4$. Tìm giá trị nhỏ nhất của \[P=\frac{4x}{3-4x^2}+\frac{4y}{3-4y^2}+\frac{4z}{3-4z^2}.\]
6. Gọi $a,b,c$ là độ dài ba cạnh của một tam giác. Chứng minh rằng \[\frac{a^{20016}}{b+c-a}+\frac {b^{2016}}{c+a-b}+\frac{c^{2016}}{a+b-c}\geq a^{2015}+b^{2015}+c^{2015}.\]
7. Cho tam giác đều $ABC$ có cạnh bằng $a$. Lấy điểm $Q$ bất kỳ trên cạnh $BC$ ($Q$ khác $B$, khác $C$). Trên tia đối của tia $BA$ lấy điểm $P$ sao cho $CQ\times AP=a^2$. Gọi $M$ là giao điểm của $AQ$ và $CP$. Chứng minh rằng bốn điểm $A, B, M, C$ cùng thuộc một đường tròn. 
8. Cho tam giác đều $ABC$ có cạnh bằng $a$. Lấy điểm $Q$ bất kỳ trên cạnh $BC$ ($Q$ khác $B$, khác $C$). Trên tia đối của tia $BA$ lấy điểm $P$ sao cho $CQ\times AP=a^2$. Gọi $M$ là giao điểm của $AQ$ và $CP$. Gọi  $I, J, K$ lần lượt là hình chiếu của $M$ lên $AB, BC, CA$. Xác định vị trí của $Q$ để độ dài $IK$ lớn nhất.
9. Cho tam giác đều $ABC$ có cạnh bằng $a$. Lấy điểm $Q$ bất kỳ trên cạnh $BC$ ($Q$ khác $B$, khác $C$). Trên tia đối của tia $BA$ lấy điểm $P$ sao cho $CQ\times AP=a^2$. Gọi $M$ là giao điểm của $AQ$ và $CP$. Gọi  $I, J, K$ lần lượt là hình chiếu của $M$ lên $AB, BC, CA$. Chứng minh rằng $MI^2+MJ^2+MK^2$ không đổi khi $Q$ thay đổi trên cạnh $BC$.
10. Cho bảng ô vuông kích thước $10\times10$ gồm 100 ô vuông kích thước $1\times1$. Điền vào mỗi ô vuông của bảng một số nguyên dương không lớn hơn 10 sao cho hai số được điền ở hai ô vuông chung cạnh hoặc chung đỉnh thì nguyên tố cùng nhau. Chứng minh rằng trong bảng ô vuông đã cho có một số số xuất hiện ít hơn 17 lần. ​